1701 Cubeditor KMP
idx(0~N-1)부터 N까지의 부분문자열에 대해 Pi를 구한다.
idx에 대하여
최대 Pi값 - idx = 두 번 이상 나오는 가장 긴 부분문자열의 길이
* Pi를 구하는 시작점의 인덱스가 0이 아님에 주의해서 풀면 됨

16900 이름 정하기 KMP
주어진 문자열 S가 최소 K번 부분문자열로 등장하는 새로운 문자열 길이의 최솟값을 구한다.
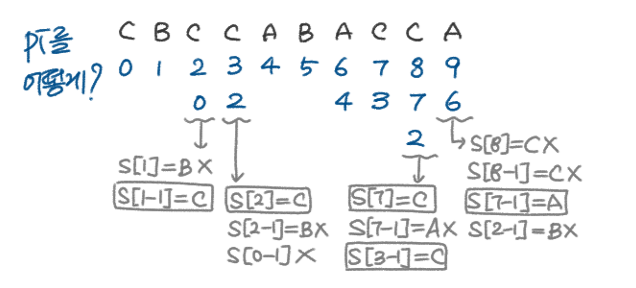
Pi를 구해 문자열 S에서 K-1번 반복해줄 부분 문자열을 구한다. 아래는 예시
S ada 3
pi 001 => (3-2)+2*3
S abc 2
pi 000 => (3-3)+3*2
S rr 5
pi 01 => (2-1)+1*5
S abcabcabca 3
pi 0001231234 => (10-3)+3*3
1509 팰린드롬 분할 DP
주어진 문자열을 팰린드롬으로 분할할 때 분할 개수의 최솟값
분할하는 경우의 수가 아닌, 분할했을 때 나눠진 부분문자열의 개수의 최솟값을 구하는 거
dp[0] = 1;
for (int cur = 1; cur < N; ++cur) {
dp[cur] = cur + 1;
for (int prv : pi[cur]) {
if(prv) dp[cur] = min(dp[cur], dp[prv-1] + 1);
else { dp[cur] = 1; break; }
}
}

근데 pi[i]가 하나의 값이 아니라,, 벡터여야 한다.
i를 포함하는 팰린드롬의 개수가 여러개일 수 있고 무조건 길이가 긴 팰린드롬이 최선의 선택은 아닐 수 있기에
2533 사회망 서비스(SNS) DP Tree
* 처음에 일반적인 트리나 그래프 문제로 생각했는데,, DP였다
Queue, Stack모두 이용해 탐색할 노드를 자식부터 Stack에 넣는다.
* Queue에서 vis배열의 초기화에 주의한다.
dp[ v ][ 0 ]은 v가 얼리어답터가 아닐 때 v를 루트로 하는 트리 모두가 얼리어답터가 되기 위한 최소 얼리어답터 수
dp[ v ][ 1 ]은 v가 얼리어답터일 때 "

11505 구간 곱 구하기 Segment Tree
* Update를 잘못 생각해서 몫과 나머지 모두 저장하는 세그먼트 트리를 만드려고 했었따... (바뀐 수에 대해 곱의 차를 더해주려고 했음) 당연히 몫이 수의 범위를 초과해 저장할 수 없었음. 잘못 생각했음을 깨닫고 편안하게 구간 곱을 mod로 구해놓은 세그먼트트리로 바꿈
1615 교차개수세기 Segment Tree Fenwick Tree
일반적인 inversion세는 문제
inversion은 팬윅 트리로 짜는 게 더 편하고 이해도 잘 돼서 세그먼트 트리로는 구현 안해봤는데,, 생각 해보긴 해야겠다.
간선 a b를 a 기준으로 정렬하고 순서대로 Update, Sum을 호출해 답을 구하면 된다.
매 간선마다, 이전에 b보다 큰 값이 나온 횟수를 생각하자

1766 문제집 그래프 위상정렬
* 아래 그림에서 5의 경우 4와 7을 모두 풀어야 풀기 쉬운 문제가 된다. inord값을 한 개씩 빼줘야지 저쪽에 접근하게됐다고 바로 0으로 만들어버리면 안 된다,, 휴 첨에 이거 실수함 너무 간단하게 생각했어

20040 사이클게임 그래프 Disjoint Set
Union Find 잘 하면 됨

2254 감옥 건설 기하학 Convex Hull CCW
Convex Hull 공부하고 푼 문제
볼록 껍질 만드는 것도 만드는 거지만 점 P가 그 안에 속해있는지도 확인해야 했다.
CCW를 이용해 확인할 수 있다. P를 시점으로 convex hull의 꼭짓점을 종점으로 하는 이웃한 벡터 간 각이 시계방향으로만 흘러가면 점 P는 그 안에 존재한다.
구현이 매우,, 복잡했던 생각이 난다. 컨벡스헐은 헷갈리지만 않으면 된다.

필기는 바로바로 옮겨놔야지 미루면 안 돼..!
'Probelm Solving > Notes' 카테고리의 다른 글
| 그리디 (1) (0) | 2021.05.03 |
|---|---|
| 그래프 (2) 문제들 (0) | 2021.04.26 |
| 구현 (2) 지난 주 푼 문제 (0) | 2021.04.05 |
| 그래프 (1) 최근 푼 문제 (0) | 2021.03.15 |
| 기하학 (2) 계산 문제들 (0) | 2021.03.15 |
댓글