SDBMS 공간데이터베이스
⑤ The z-Ordering Tree
0. Z-Ordering
여러 개의 quadrant를 이용하여 하나의 다각형을 mbb가 아닌 형태로 나타낼 수 있다.

degree=3으로 공간을 나눈 경우 가장 작은 quadrant는 전체 공간의 1/64 크기가 되고 label 길이는 3이 된다.
이때 도형 A의 경우 위처럼 표현할 수 있다.
만약 degree=2로 공간을 나눴다면 A={01,02,03,12,20,21,23,31}가 된다.
이런 방식으로 객체 정보를 저장하고 인덱싱 한 게 Z-Ordering Tree이다.
1. The Z-Ordering Tree
Z-Ordering tree는 linear quadtree와 마찬가지로 quadrant의 label을 key로 하는 B+tree를 사용한다.
그러나 quadrant를 나눌 때 degree를 기준으로 나눠 최소 quadrant 크기에 한계가 있다는 점에서 차이가 있다.
Linear quadtree: quadrant 내에 객체의 수가 많아지면 해당 quadrant를 사분할
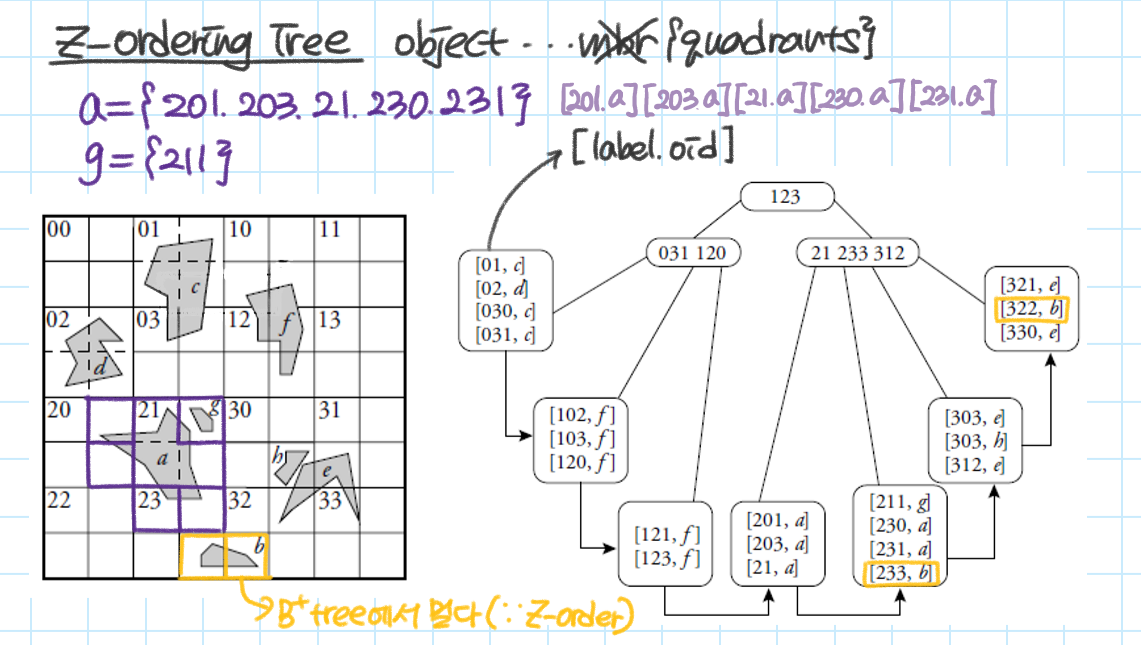
Z-Ordering Tree는 각 객체를 [quadrant label, oid]로 표현한 데이터를 B+tree로 관리한다.
이때 객체 a와 g가 모두 존재하는 quadrant(211)가 있지만
a는 210,211,212,213에 모두 존재하기 때문에 해당 quadrant를 합쳐 21로 표현하게 되고
g는 211에만 존재하기 때문에 211로 표현한다.
같은 quadrant에 존재해도 그 범위가 다르게 표현될 수 있기 때문에 linear quadtree보다 정밀한 쿼리 처리를 할 수 있다.
* Query
Window query, W(x1,y1,x2,y2)
begin
result = {}
l1=PointLabel(x1,y1) // Compute label of NW, SE point
l2=PointLabel(x2,y2)
L1=MaxInf(l1)
L2=MaxInf(l2)
Q=Range([L1,L2]) // Get the entries of label L1~L2
for each e in Q do
if(W INTERSECT Quadrant(e)) then reault+=(e.oid)
end for
Sort(result), RemoveDupl(result)
return result
endQ를 구하는 것까지(~line 9)는 linear quadtree와 같다.
입력 범위의 NW, SE에 해당하는 quadrant label을 구하고 해당 범위 내에 존재하는 entry를 모두 Q에 저장한다.
이후 Q의 각 원소마다 W와 e의 quadrant가 겹치면 result에 포함하여 결과를 얻어낸다.
IO Count = 3d+k
아래에서 02와 211을 구하면서 +2*3, Q를 구하면서 +3+5
(degree=3, 탐색한 B+tree의 leaf 개수가 5개)

! 여기서 위 알고리즘에 따르면 윈도우 쿼리 결과가 {a,c,d,g}로 나오는 게 맞는 듯. g는 false drop으로 refinement step에서 걸러져야 한다.
* Z-Ordering Tree VS Linear Quadtree

Z-Ordering Tree
- 공간을 degree를 기준으로 나누어 최소 quadrant 크기에 한계가 있다.
- 더 세분화한 표현이 가능해 더 정밀한 쿼리 처리를 할 수 있다.
- 한 객체에 해당하는 quadrant 수가 많아져 entry 개수가 늘어난다.
Linear Quadtree
- 한 quadrant 내 객체의 수가 많아지면 quadrant를 사분할한다.
- 상대적으로 entry 수가 적다.
- 그만큼 쿼리 처리 능력이 떨어진다.
2. A Raster Variant of Z-Ordering (with Redundancy)
Quadrant의 크기를 통일하여 나타낼 수도 있다.

그러나 이런 분할은 entry 수가 많아져 B+tree가 커진다는 단점이 있다.
Z-Ordering Tree에서는 a={201,203,21,230,231}로 표현했지만
셀의 크기를 모두 같게 하면 21대신 210,211,212,213으로 a를 표현해야 한다.
장점은 알고리즘이 간단해진다는 것.
Quadrant의 크기가 동일하기 때문에 label 길이가 모두 같아 비교함수가 간단해지며
Window 쿼리의 경우 위 알고리즘에서 MaxInf 함수를 사용하는 부분을 삭제해도 된다.
3. The Z-Ordering Tree without Redundancy

한 객체에 한 quadrant를 대응하여 저장할 수도 있다.
해당 객체를 포함하는 quadrant 중 label의 길이가 가장 짧은 것을 이용하는 방법
이 방법의 경우 한 객체에 대응되는 데이터 개수가 적어 B+tree의 entry 수가 적다는 장점이 있지만
quadrant 크기에 비해 객체의 크기가 작아 공간 낭비가 발생하고 쿼리 처리가 어렵다.
예를 들어 위 그림의 b는 quadrant 2와 3에 걸쳐있기 때문에 root를 의미하는 quadrant에 대응된다. 엄청난 손해,,
* Window Query
Label의 prefix를 이용한다. 객체마다 하나의 entry만 존재해서 중복제거를 할 필요도 없다.
begin
result={}
for each v in Prefix(W.l) do
k=Minsup(v)
while(k.l=v) or (v=W.l and W.l in Prefix(k.l)) do
result += {k,oid}
k=Next(k)
end while
end for
return result
endW.l = 0 (그림에서 W가 quadrant 0에 속한다.)
Prefix(W.l) = { _ , 0 }
v = _ : k.l = _ ⇒ result += {b}
v = 0 : k.l = 0 ⇒ result += {c}
k.l = 02 ⇒ result += {d}
without redundancy 버전은 수업에서 다루진 않았고 pdf 파일 보다가 처음 봤는데 간단히 다뤄봤다.
Z-Ordering Tree도 space-driven 구조이지만
다른 구조(grid file, linear quadtree)에 비해 좀 더 객체 중심으로 생각하게 된다.
객체에 해당하는 quadrant를 찾을 때 그렇게 생각하게 되는 듯.
이제 space-driven 구조는 KD tree만 마저 간단히 다루고
data-driven인 R-tree M-tree로 넘어갈 예정~!~!
'Study > SDBMS' 카테고리의 다른 글
| SDBMS ⑧ The R-Tree - Insert, Split (0) | 2021.08.09 |
|---|---|
| SDBMS ⑥ The KD Tree (0) | 2021.04.15 |
| SDBMS ④ The Linear Quadtree (0) | 2021.04.02 |
| SDBMS ③ SAM, The Grid File (0) | 2021.03.29 |
| SDBMS ② ER Diagram and Relational Schema (0) | 2021.03.15 |




댓글