SCC
: 강한 연결 요소 strongly connected components
그래프 내 vertex 중 서로 간의 경로가 양방향 모두 존재하는 vertex들의 집합
X⊂G s.t. ∀a, b∈X, ∃ paths both a→b, b→a
DFS와 스택이 핵심이다.
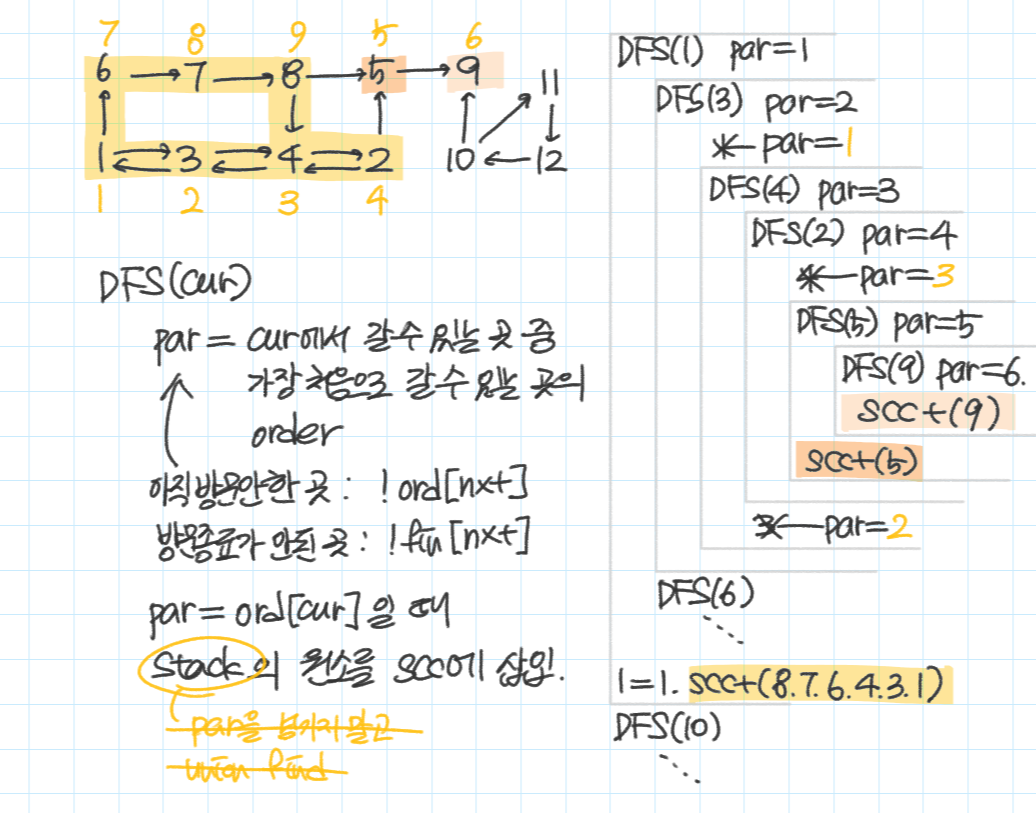
방문 지점의 order(몇 번째로 방문했는지)를 이용한다.
DFS함수의 리턴 값은 현재 노드에서 도달할 수 있는 지점 중 가장 먼저 방문한 지점의 방문 순서이다.
DFS(cur) = par = cur에서 도달할 수 있는 지점의 ord 중 최솟값
ord[v] v 방문 순서
fin[v] v 방문 완료 여부 = v가 속하는 SCC를 찾았는지?
현재 방문한 지점을 cur, 다음에 방문할 지점을 nxt라 하자. nxt는 다음 세 가지 경우 중 하나에 해당한다.
1. 아직 방문하지 않은 곳이다.
2. 방문했지만, 방문이 완료되지 않은 곳이다.
3. 이미 방문이 종료된 곳이다.
3의 경우 생각하지 않는다. 방문이 종료되었다는 건 이미 nxt가 속하는 SCC를 찾았으며, nxt에서 cur로 가는 경로가 없었다는 뜻
2의 경우 par을 현재 값과 ord[nxt] 중 최솟값으로 갱신한다.
1의 경우 B를 방문해 par을 현재 값과 DFS(nxt) 중 최솟값으로 갱신한다.
cur에서 갈 수 있는 지점을 모두 방문하면 정의에 맞는 par이 구해진다.
par과 ord[cur]이 같다면 cur이후에 방문한, S에 남아있는 지점이 cur과 SCC를 이룸을 뜻한다.
SCC를 이루는 지점에 대해서는 스택에서 삭제하고 fin을 갱신한다.
par과 ord[cur]이 같지 않으면 SCC를 찾기에는 시기상조이다. 스택에 cur을 넣어둔 채로 DFS를 종료한다.
int DFS(int cur) {
ord[cur] = ++num; S.push(cur);
int par = ord[cur];
for (int nxt : e[cur]) {
if (!ord[nxt]) par = min(par, DFS(nxt));
else if (!fin[nxt]) par = min(par, ord[nxt]);
}
if (par == ord[cur]) {
vector<int> scc;
while (1) {
int v = S.top(); S.pop();
scc.push_back(v); fin[v] = true;
if (v == cur) break;
}
sort(scc.begin(), scc.end());
SCC.push_back(scc);
}
return par;
}
1.
단순히 ord[nxt]가 ord[cur]보다 크니 line5 에서 par을 갱신하지 않고 DFS를 수행해도 된다고 생각했다. 당연히 틀렸고
A→B→C→A와 같은 경로가 있다면 ord[A]=1, ord[B]=2, ord[C]=3이지만 DFS(C)=1(line 6)이 되어 DFS(B)에서 par을 갱신해야 한다(line 5). par의 정의를 명확히 알고 있어야 한다.
2.
SCC를 들어보기는 했으나 구현은 처음이었다. 고민해 구현한 코드는 시간초과였고 다른 블로그를 참고해 어떤 식으로 동작하는지 파악해 현재 코드를 배울 수 있었따..
3.
1월 알고리즘 캠프에서 단절점, 단절선 배울 때 이 개념 응용해서 SCC에 적용할 수 있다는 말은 들었다.
그래서 방문 순서 기록, 부모 노드를 매개변수로 넘겨줬던 걸 차용해 구현했지만 시간초과. 심지어 내 코드에선 1) union을 계속 해줘야했고 2) 이것저것 확인하는 배열도 많이 쓰고 3) SCC 정렬도 비효율적으로 흘러가 엄청난 시간초과였다. 고민해보는 건 좋은 시도였겠지만

BOJ2150을 풀면서 공부하게 됐다. 아래는 전체 코드와 예시
#include <cstdio>
#include <vector>
#include <stack>
#include <algorithm>
using namespace std;
int num = 0, ord[100001];
bool fin[100001];
vector<int> e[100001];
vector<vector<int>> SCC;
stack<int> S;
bool sortscc(vector<int> A, vector<int> B) {
return A[0] < B[0];
}
int DFS(int cur) {
ord[cur] = ++num;
S.push(cur);
int par = ord[cur];
for (int nxt : e[cur]) {
if (!ord[nxt]) par = min(par, DFS(nxt));
else if (!fin[nxt]) par = min(par, ord[nxt]);
}
// par: the minimal order of vertices connected to cur
// !ord[nxt] not visited yet (nxt which might be connected to prv)
// !fin[nxt] visited but not finished (prv which is connected to cur)
// Assume: visit order: prv -> cur -> nxt
if (par == ord[cur]) {
vector<int> scc;
while (1) {
int v = S.top(); S.pop();
scc.push_back(v); fin[v] = true;
if (v == cur) break;
}
sort(scc.begin(), scc.end());
SCC.push_back(scc);
}
return par;
}
int main() {
int V, E, u, v;
scanf("%d%d", &V, &E);
while (E--) {
scanf("%d%d", &u, &v);
if (u != v) e[u].push_back(v);
}
for (int i = 1; i <= V; ++i) if (!ord[i]) DFS(i);
sort(SCC.begin(), SCC.end(),sortscc);
printf("%d\n", SCC.size());
for (vector<int> scc : SCC) {
for (int v : scc) printf("%d ", v);
printf("-1\n");
}
return 0;
}
/*
10 14
1 3 3 1 3 4 4 2 4 3 2 4 10 9
1 6 6 7 7 8 8 4 8 5 5 9 2 5
12 17
1 3 3 1 3 4 4 2 4 3 2 4 10 9 10 11 11 12 12 10
1 6 6 7 7 8 8 4 8 5 5 9 2 5
*/
'Probelm Solving > Algorithm' 카테고리의 다른 글
| Euler phi function 오일러 피 함수 (0) | 2021.04.16 |
|---|---|
| Segment Tree (0) | 2021.04.15 |
| Convex Hull과 CCW (0) | 2021.04.09 |
| KMP (0) | 2021.04.09 |
| 행렬의 제곱 (0) | 2021.01.16 |




댓글