Euler phi function
오일러 피 함수
$\varphi \left ( n \right )$
= $n$ 이하 자연수 중 $n$ 과 서로소인 수의 개수
소수 $p$와 자연수 $a$에 대하여 다음을 만족한다.
$\varphi \left ( p \right )=p-1$
$\varphi \left ( p^a \right )=p^a-p^{a-1}={p^a} \left ( 1-\frac{1}{p} \right ) $
또한 $\left ( m,n \right )=1$ 인 두 자연수 $m$, $n$에 대하여
$\varphi \left ( mn \right )=\varphi \left ( m \right ) \varphi \left ( n \right ) $
따라서 소수 $p$, $q$와 자연수 $a$, $b$에 대하여
$\varphi \left ( {p^a}{q^b} \right )=\left ( {p^a}-{p^{a-1}} \right )\left ( {q^b}-{q^{b-1}} \right )={p^a}\left ( 1-\frac{1}{p} \right ){q^b}\left ( 1-\frac{1}{q} \right )$
이다.
$N$의 오일러 피 함숫값을 구하려면 먼저 $N$을 소인수 분해해야 한다.
$N$을 소인수 분해하기 위해서는 $N$ 보다 작은 소수를 찾아야 한다.
그러나 굳이 모든 소수를 찾을 필요는 없다.
$\sqrt{N}$ 이하의 소수만 찾으면 $\sqrt{N}$보다 큰 소수는 저절로 구해지게 되어있음
따라서 아래와 같이 1. 소수를 찾아 $N$의 소인수만 벡터(prime)에 저장하고
for (long long i = 2; i <= sqrt(N); ++i) {
if (!notp[i]) {
if (!(N % i)) prime.push_back(i);
for (long long j = i * i; j <= 1000000; j += i) notp[j] = true;
}
}
2. 반복문으로 오일러 피 함숫값을 계산하면 된다.
long long euler_phi = 1;
for (long long p : prime) {
int a = 0;
while (!(N % p)) {
a++, N /= p;
}
euler_phi *= ((p - 1) * pow(p, a - 1));
if (N == 1) break;
}
if (N > 1) euler_phi *= (N - 1);소인수로 $N$을 계속 나눈 결과 값이 1보다 크다면 그 값이 $\sqrt{N} $ 보다 큰 소인수라는 뜻이다.
납득이 안 된다면 ${2^3}{3^1}{53^1}=1272$, $\sqrt{1272}=33.665...$를 떠올려보자
11689 GCD(n,k)=1 을 풀면서 정리함
계속 소수 구하는 걸 잘 못했는데 같이 정리된 듯
$\sqrt{N}$ 이하의 소수만 구해도 됨을 기억하자
19577 수학은 재밌어가 더 어려운 것 같은데 왜 티어는 이게 낮은지
이건 주어진 $n$에 대하여 $x\varphi \left ( x \right )=n$을 만족하는 최소의 자연수 $x$를 구하는 문제다.
$\varphi \left( x \right )$값이 $x$보다 작다는 점을 이용해
$\sqrt{N}$보다 큰 $N$의 약수를 $x$로 하고 오일러 피 값을 구해 비교하며 알맞은 $x$를 찾으면 된다.
증명
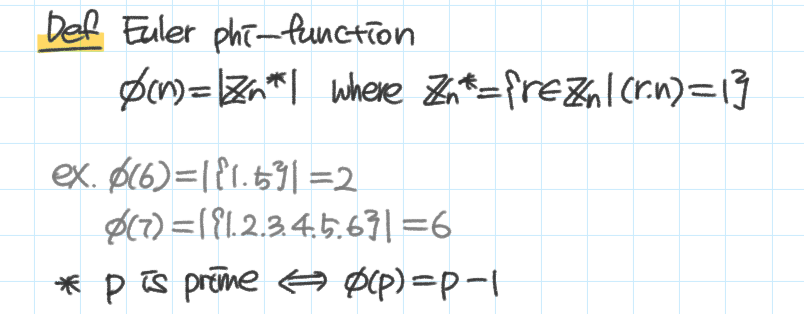
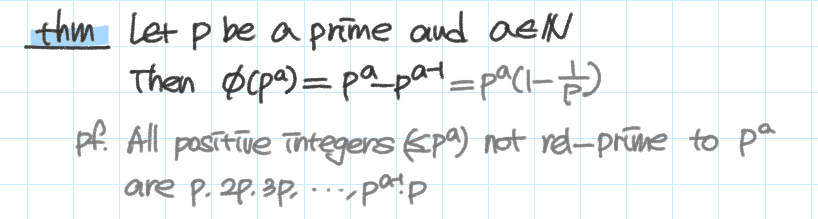
Def. $f$ is multiplicative
⇔ $f\left ( mn \right )=f\left ( m \right )f\left ( n \right ) $ where $\left ( m,n \right )=1$


'Probelm Solving > Algorithm' 카테고리의 다른 글
| Lazy Propagation (1) | 2021.08.13 |
|---|---|
| ETT 오일러 경로 테크닉, 근데 이제 펜윅을 곁들인 (2) | 2021.08.05 |
| Segment Tree (0) | 2021.04.15 |
| SCC (0) | 2021.04.13 |
| Convex Hull과 CCW (0) | 2021.04.09 |




댓글