Euler Tour Technique
오일러 경로 테크닉
트리의 한 간선을 양방향 간선(or 반대 방향의 간선 두 개)로 생각한 뒤
루트에서 출발해 루트로 도착하는 그래프(트리)의 오일러 사이클을 찾는 것으로
트리를 표현하는 방식이다.
* 오일러 사이클은 시작점=종점인 한붓그리기로 이해하면 됨
이렇게

144125566788997233
255667889972144133
255799887662331441 등...
트리가 주어지고 다음과 같은 쿼리가 주어진다고 하자.
1. i번 노드의 모든 하위 노드(자식, 자식의 자식...)의 값을 w만큼 증가한다.
or i번 노드의 모든 상위 노드(부모, 부모의 부모...)의 값을 w만큼 증가한다.
2. i번 노드의 값을 출력한다.
DFS로도 가능이야 하지만 트리의 깊이가 깊다면 한계가 있다.
ETT를 펜윅/세그먼트 트리와 함께 사용하면
위 같이 어떤 노드의 모든 상위/하위 노드에 대한 쿼리를 수월하게 처리할 수 있다.
먼저 오일러 사이클에 따라 각 노드에 도착한 시간과 노드를 떠난 시간을 구하자.
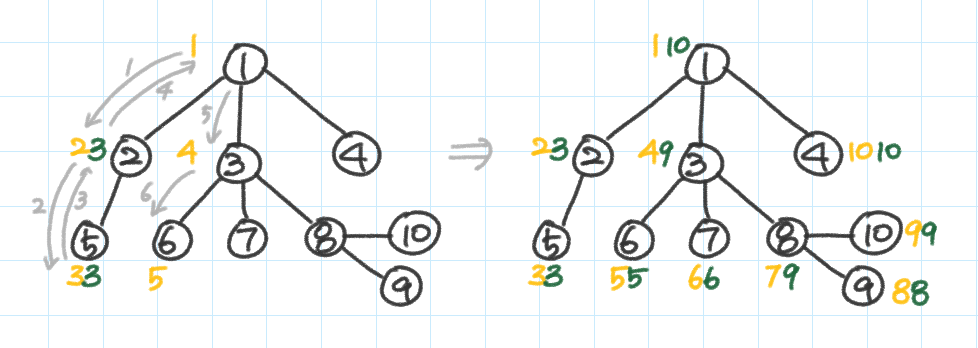
각 노드에 대해 도착한 시간을 in, 떠난 시간을 out 배열에 저장하자.
4, 5번 노드와 같이 자식 노드가 없는 경우 in과 out이 동일하다.
3번 노드의 경우 in[3]=4, out[3]=9이고, 이때 3번 노드의 모든 하위 노드의 in은 4<in≤9를 만족한다.
8번 노드에서도 마찬가지.
즉, in[B] < in[A] ≤ out[B] ⇔ A는 B의 어떤 하위 노드이다.
각 노드의 in, out은 간단한 DFS로 구한다.
vector<int> e[N];
int cnt = 0;
void dfs(int cur){
in[cur] = ++cnt;
for(int nxt : e[cur]) dfs(nxt);
out[cur] = cnt;
}
이제 각 노드에 해당하는 값을 배열에 저장한다.
이때 위의 부모-자식 간 관계를 이용하기 위해 in을 활용한다.
a[노드 번호]=노드의 값 으로 하지 않고
a[노드의 in]=노드의 값 으로 한다.
ex) 5번 노드의 값을 a[5]가 아닌 a[3]에 저장한다.
펜윅/세그먼트 트리를 이용해 구간 합을 저장하여 다음 쿼리를 처리하자.
1. Q(i,w) i번 노드의 모든 자식 노드의 값을 w만큼 증가한다.
펜윅 트리의 sum(in[n]) = n번 노드 값의 변화량이 되도록 한다.
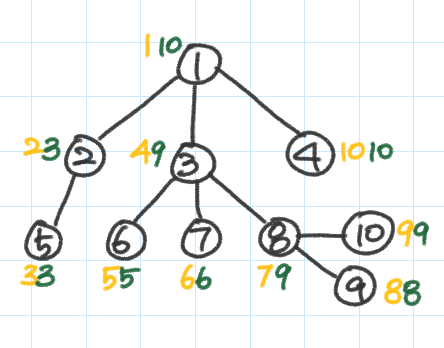
Q(3,7)의 경우 a[4]~a[9]의 값을 7만큼 증가시켜야 한다.
이 쿼리를 update(4,7), update(9+1,-7) 으로 처리한다.
* 당연히 연속적으로 처리하면 시간이 너무 오래 걸린다...
Q(3,7), Q(2,5), Q(8,3) 을 순서대로 시행하는 과정을 표로 이해해보자.
여기서 sum(8)이 Q(2,5)의 영향을 받지 않음을 이해해야 한다.
각 쿼리 처리 후 9번 노드의 값은 a[9]+sum(8)이다.
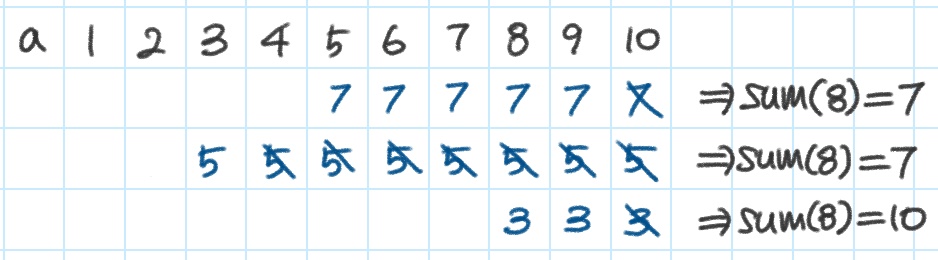
* 표는 배열 a 시점인데 펜윅 트리 상에서 이해해보자.. 이보다 나은 표현을 못 찾음
BOJ2820 자동차 공장이 이런 문제
line 14~17 update를 두 번 하는 것보다는 한 번의 호출로 끝내는 함수를 사용했다.
#include <iostream>
#include <vector>
using namespace std;
int fen[500001];
int in[500001], out[500001], cnt;
vector<int> e[500001];
void dfs(int cur) {
in[cur] = ++cnt;
for (int nxt : e[cur]) dfs(nxt);
out[cur] = cnt;
}
void upd_(int i, int j, int x) {
while (i < cnt) fen[i] += x, i += (i & -i);
while (j < cnt) fen[j] -= x, j += (j & -j);
}
int sum_(int i) {
int ret = 0;
while (i) ret += fen[i], i -= (i & -i);
return ret;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int a[500001];
int N, M, i, x, sup;
char q;
cin >> N >> M;
cin >> a[1];
for (i = 2; i <= N; ++i) cin >> a[i] >> sup, e[sup].push_back(i);
dfs(1); ++cnt;
while (M--) {
cin >> q >> i;
if (q == 'p') {
cin >> x;
upd_(in[i] + 1, out[i] + 1, x);
}
else cout << a[i] + sum_(in[i]) << "\n";
}
return 0;
}
2. Q(i,w) i번 노드의 모든 상위 노드의 값을 w만큼 증가한다.
이때는 펜윅 트리의 sum(out[n])-sum(in[n]-1) = n번 노드 값의 변화량이 되도록 한다.

따라서 Q(8,6)의 경우 update(7,6)으로 처리한다.
마찬가지로 Q(8,6), Q(2,2), Q(6,-1) 을 순서대로 시행하는 과정은 아래와 같고
각 쿼리 처리 후 3번 노드의 값은 a[3]+sum(8)-sum(4-1)이다.
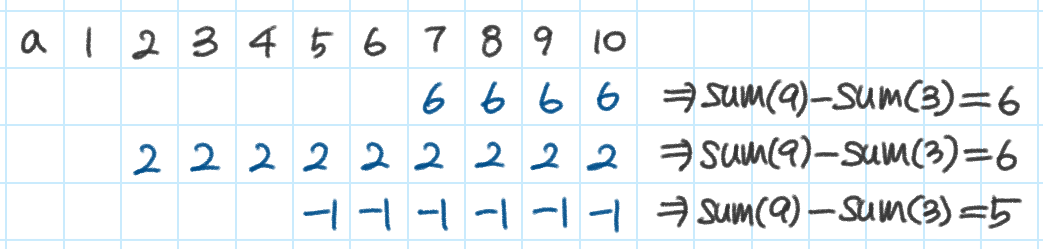
BOJ14287 회사 문화 3이 이런 문제
#include <iostream>
#include <vector>
using namespace std;
int fen[100010];
int in[100001], out[100001], cnt;
vector<int> e[100001];
void dfs(int cur) {
in[cur] = ++cnt;
for (int nxt : e[cur]) dfs(nxt);
out[cur] = cnt;
}
void upd_(int i, int w) {
while (i < cnt) fen[i] += w, i += (i & -i);
}
int sum_(int i) {
int ret = 0;
while (i) ret += fen[i], i -= (i & -i);
return ret;
}
int main() {
ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);
int N, M, q, id, w;
cin >> N >> M >> id;
for (int i = 2; i <= N; ++i) cin >> id, e[id].push_back(i);
dfs(1); ++cnt;
while (M--) {
cin >> q >> id;
if (q & 1) cin >> w, upd_(in[id], w);
else cout << sum_(out[id]) - sum_(in[id] - 1) << "\n";
}
return 0;
}
ETT 자체보다는 이걸 펜윅 트리에서 어떻게 쓸 거냐가 관건이다.
하위 노드를 처리하는 방식과
상위 노드를 처리하는 방식이 좀 달라서 글 쓰면서도 너무 헷갈렸는데
sum으로 뭘 구하느냐를 명확히 해야겠음.
사실 아직 상위/하위로 한 문제씩만 풀어봤다.
하위의 경우 저게 최선인지도 잘 모르겠다;; 더 좋은 방법이 있을런지;;
회사 문화 문제들을 연습하는 게 좋겠다.
풀다 보니 미뤄둔 lazy propagation도 이해해야 할 것 같다,, 이번 주 안으로 공부하는 걸 목표로 잡아보자...
'Probelm Solving > Algorithm' 카테고리의 다른 글
| Lazy Propagation (1) | 2021.08.13 |
|---|---|
| Euler phi function 오일러 피 함수 (0) | 2021.04.16 |
| Segment Tree (0) | 2021.04.15 |
| SCC (0) | 2021.04.13 |
| Convex Hull과 CCW (0) | 2021.04.09 |




댓글